RSA的算法：

1.任意选取两个不同的大素数p和q计算乘积n=p$\times$q

利用欧拉函数求出与n互质的数的个数$\varphi$(n)=(p-1)$\times$(q-1)

==欧拉函数:==

欧拉函数的定义：

欧拉函数(Euler’s totient function),即为$\phi$(n),是小于 n 且与 n 互质的数的个数

例如$\varphi$(7)=6,因为与7互质的数有1，2，3，4，5，6。所以只要n为素数则$\varphi$(n)=n-1

2.任意选取一个大整数e满足gcd(e,$\phi$(n))=1,整数e用作==加密钥==（1<e<$\phi$(n)）

3确定解密钥d，满足(ed) mod $\varphi$(n) = 1,即ed = k $\times$$\varphi$(n) +1,k$\geq$1是一个任意整数

4.公开整数n和e，秘密保存d

5.将明文m加密为密文c的算m法为：

c=m^e^modn

6.将密文c转换为明文m的算法为:

m=c^d^modn

证明：
m = c^d^ mod n
因为 c = m^e^ mod n
将其带入: m = (m^e^ mod n)^d^ mod n
= m^ed^ mod n
又因为： ed=k×phi_n+1
所以: m=m×m^k×phi_n^ mod n
又因为：m^k×phi_n^ = (m^k^) ^phi_n^

根据费马小定理：如果若存在整数 a , p 且gcd(a,p)=1,即二者互为质数，则有a^(p-1)^≡ 1(mod p)

又因为与n可以整除的数只有(p,q,1,n),而 m^k^ 不可能为其中一个

所以 m^k×phi_n^ mod n =1

所以证明：m=c^d^modn

==已知p,q,e,n.求私钥d。==

==以下是python源代码:== 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import gmpy2#导入gmpy2模块                 
p =gmpy2.mpz()
q =gmpy2.mpz()
e =gmpy2.mpz()
phi_n= (p - 1)*(q - 1)
d = gmpy2.invert(e, phi_n)#求逆元
print("d is:")
print (d)
求私钥d.
#在已知密文c的情况下
#则明文m等于:
m=pow(c,d,n)%n
#最后可以导入模块解题:
from Crypto.Util.number import bytes_to_long
from Crypto.Util.number import long_to_bytes
c= 
bytes = long_to_bytes(data)
print(bytes)（加密黑客的源码）
1

==RSA共模攻击==

已知c1,c2,e1,e2,n,共模攻击: 即用两个及以上的公钥(n,e)来加密同一条信息m

因为c1=m^e1^mod n,c2=m^e2^mod n

思路：我们求明文m，仿佛就在眼前，却无力回天；我们试着将c1和c2相乘；得到：c1c2=m^e2+e2^mod n

想办法让m的幂次为1则求出m，由此想到欧几里得算法

扩展欧几里得算法：ax1+by1=gcd(a,b)

设e1,e2为素数，则gcd(e1,e2)=1;

所以推导公式为：m=c1^s1^c2^s2^mod n

​ =m=c1^s1^c2^s2^mod n=m^e1s1^^+^^e2s2^mod n

以下是源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import libnum   
import gmpy2    

n = ...
c1 = ...
c2 = ...
e1 = ...
e2 = ...

s = gcdext(e1,e2)    #gmpy2.gcdext(),扩展欧几里得算法，返回tuple元组，满足s[1]*e1+s[2]*e2=1

m = pow(c1,s[1],n)*pow(c2,s[2],n)%n 

print(m)
hex_m=hex(m) #把m十进制数字转化成十六进制
print(hex_m)
import binascii
mingwen=binascii.unhexlify('666c61677b34396439313037376131616263623134663161396435343663383062653965667d')
print (mingwen)

==rsa dp，dq泄露==

已知 dp, dq,c,p,q求明文m：

RSA中已知dq，dp,p,q的计算m步骤（dp = d mod (p-1),dq = d mod (q-1)）：

(1).计算q模p的逆元 I ;

(2).计算m1 = (c^dp^) mod p;

(3).计算m2 = (c^dq^) mod q;

(4).计算m=( ( ( (m2-m1) $\times$ I) %q )$\times$ p + m1 ) % n

以下是证明:

以下是python源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
import gmpy2
dp= ...
dq= ...
c= ...
p= ...
q= ...
n=q*p
m1=pow(c,dp,p)
m2=pow(c,dq,q)
I=gmpy2.invert(p,q)
m=((((m2-m1)*I)%q)*p+m1)%n
print(m)

==dp泄露==

关键公式

1.已知n，e，dp

2.dp e= ed mod (p-1)

以下是大哥的笔记:

以下是源代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import gmpy2
e = ...
n = ...
dp = ...
c = ...

for i in range(1,e):                   #在范围(1,e)之间进行遍历
    if(dp*e-1)%i == 0:
        if n%(((dp*e-1)//i)+1) == 0:   #存在p，使得n能被p整除
            p=((dp*e-1)//i)+1
            q=n//(((dp*e-1)//i)+1)
            phi=(q-1)*(p-1)            #欧拉定理
            d=gmpy2.invert(e,phi)         #求模逆
            m=pow(c,d,n)               #快速求幂取模运算
            print(m)       #16进制转文本

#==给出公钥和密文.enc文件求解明文==

解题步骤:

1.在线Rsa 公私钥分解 Exponent、Modulus，Rsa公私钥指数、系数(模数)分解求e，n

2.然后用factordb.com求p,q的工具求出p，q

3，写脚本解密.enc文件

以下是python源代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import gmpy2
import rsa

e=65537
n=86934482296048119190666062003494800588905656017203025617216654058378322103517
p=285960468890451637935629440372639283459
q=304008741604601924494328155975272418463

phin=(q-1)*(p-1)
d=gmpy2.invert(e,phin)

key=rsa.PrivateKey(n,e,int(d),p,q)   #这里是求私钥

with open("#文件路径","rb+")as f:  #这里是打开.enc文件
 f=f.read()#阅读.enc文件
print(rsa.decrypt(f,key))#解密.enc文件f是密文，key是私钥。
#强调一定要把需要解密的文件拖到pycharm中

==低加密指数攻击==

题目情况: 当e指数特别小时，

以下是python源代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#python3
## -*- coding: utf-8 -*-#
from gmpy2 import iroot
import libnum
e = .
n = ...
c = ...
k = 0
while 1:
    res = iroot(c+k*n,e)  #c+k*n 开3次方根 能开3次方即可
    print(res)
    #res = (mpz(13040004482819713819817340524563023159919305047824600478799740488797710355579494486728991357), True)
    if(res[1] == True):
        print(libnum.n2s(int(res[0]))) #转为字符串
        break
    k=k+1
#b'flag{25df8caf006ee5db94d48144c33b2c3b}'

==共素数攻击==

共用素指数e，不同的n和c

以下是源代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
from gmpy2 import gcd,invert
from libnum import n2s
e = 65537
n1 = ...
c1 = ...
n2 = ...
c2 = ...
q = gcd(n1, n2)
p = n1//q
r = n2//q
print(n2s(pow(c1, int(invert(e, (p-1) * (q-1))), n1)).decode(), end = "")
print(n2s(pow(c2, int(invert(e, (r - 1) * (q - 1))), n2)).decode(), end="")
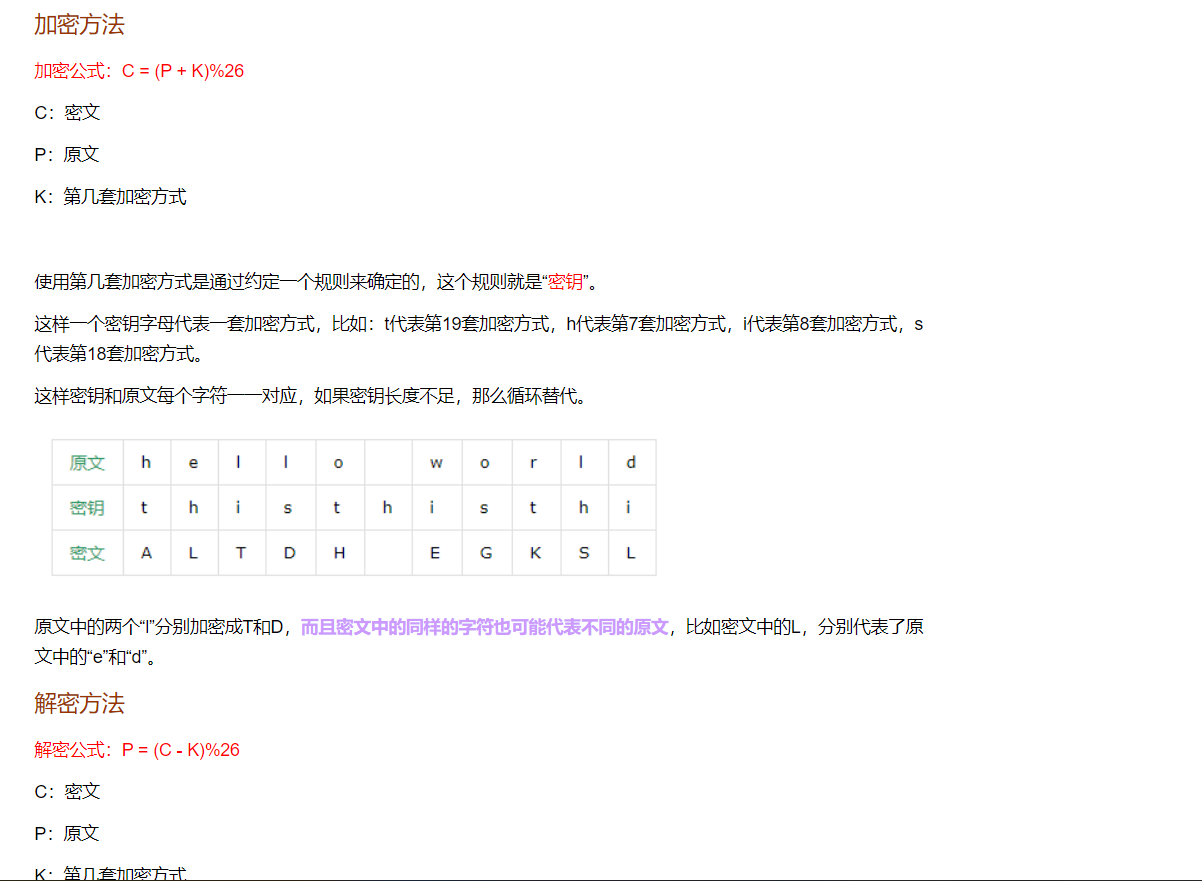
#求私钥d的时候大整数n不同所以不易求欧拉函数；因此我们可以求n1和n2的最大公约数，然后随便选取一个n1或n2来除以最大公约数q；最后用r或者用p求出来的欧拉函数都相同。

==维吉尼亚加密和解密==

维吉尼亚加密解密原理：

以下是加密源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def encrypt(message,key):#加密
    cipher = ''
    non_alpha_count = 0
    for i in range (len(message)):#遍历
        if message[i].isalpha():
            if message[i].islower():
                offset = ord(key[(i - non_alpha_count) % len(key)]) - ord('a')
                cipher += chr((ord (message[i]) - ord('a') + offset) % 26 + ord('a'))
            else:
                offset = ord(key[(i - non_alpha_count) % len(key)]) - ord('a')
                cipher += chr((ord (message[i]) - ord('A') + offset) % 26 + ord('A'))
        else:
            cipher += message[i]
            non_alpha_count += 1
    return cipher
message='YzBibXZnaHl6X3swUmF6X2d4eG0wdGhrem9fMG9iMG1fdm9rY2N6dF8hcn0='
key='hgame'
print(encrypt(message,key))

以下是解密源代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def decrypt(cipher,key):#解密
    message = ''
    non_alpha_count = 0
    for i in range (len(cipher)):#遍历
        if cipher[i].isalpha():
            if cipher[i].islower():
                offset = ord(key[(i - non_alpha_count) % len(key)]) - ord('a')
                message += chr((ord (cipher[i]) - ord('a') - offset) % 26 + ord('a'))
            else:
                offset = ord(key[(i - non_alpha_count) % len(key)]) - ord('a')
                message += chr((ord (cipher[i]) - ord('A') - offset) % 26 + ord('A'))
        else:
            message += cipher[i]
            non_alpha_count += 1
    return message
cipher="FfBufEFnmLs6D3siYtL6X2p4iN0cdSlykm9rQN9oMS1jks9rK2R6kL8hor0="
key="hgame"
print(decrypt(cipher,key))